Principal

Uma idade para a Lua pode ser determinada pela datação de um processo que resulta no fracionamento químico de elementos pais e filhos de um cronômetro de radionuclídeos adequado e que pode ser intimamente ligado à formação da própria Lua. Um desses processos é a cristalização do oceano de magma lunar (LMO), que levou à separação impulsionada pela densidade de cumulados máficos iniciais que afundaram no fundo de cumulados ricos em plagioclásio flutuantes que flutuaram para o topo do LMO, formando os anortositos ferrosos (FANs) que dominam a crosta lunar 15 . A cristalização do LMO produziu um líquido residual denominado KREEP (para fortes enriquecimentos em potássio, elementos de terras raras e fósforo), cuja formação é frequentemente usada para marcar o fim da solidificação do LMO 15 . As idades dos produtos distintos de formação inicial e tardia do LMO são notavelmente consistentes e todos dão uma idade de aproximadamente 4,35 bilhões de anos atrás (Ga), incluindo (1) as idades de cristalização mais confiáveis ​​de FANs, (2) as idades modelo de 147 Sm– 143 Nd e 176 Lu– 176 Hf de KREEP, (3) uma isócrona de rocha inteira de 146 Sm– 142 Nd de FANs, basaltos de mares (que se formaram pela refusão dos cumulados máficos do LMO) e KREEP, e (4) idades de cristalização da suíte magnesiana (suíte Mg; que representa derretimentos intrudidos na crosta anortosítica formada anteriormente) (veja o resumo das idades na ref. 16 ). Essas idades foram interpretadas para refletir a rápida cristalização do LMO e a formação tardia da Lua em aproximadamente 4,35 Ga (refs. 2 , 4 , 16 ). No entanto, os modelos de evolução térmica preveem uma solidificação mais prolongada do LMO, e interpretar as idades mencionadas acima dentro da estrutura de tais modelos leva a uma formação estimada mais precoce da Lua em 4,425 ± 0,025 Ga (ref. 17 ). De qualquer forma, essas jovens idades propostas são problemáticas por dois motivos. Primeiro, elas são tardias em comparação com as previsões da maioria dos modelos dinâmicos de formação de planetas 11 , 18. Segundo, elas são inconsistentes com a ocorrência de zircões lunares raros com idades mais antigas 5 , 7 e composições isotópicas de háfnio indicativas de derivação de uma fonte KREEP que pode ter se formado já em cerca de 4,5 Ga (ref. 6 ), o que implica que a Lua teria se formado ainda mais cedo. As idades iniciais de formação da Lua foram propostas com base em um modelo de rubídio-estrôncio de aproximadamente 4,51 Ga para perdas voláteis da Lua 19 e um modelo de idade de háfnio-tungstênio (Hf-W) de aproximadamente 4,52 Ga para a formação do núcleo lunar 20 , mas a veracidade de ambas as idades é debatida21 , 22 . No entanto, se a Lua se formou cedo, então o agrupamento de aproximadamente 4,35 Ga de idades lunares deve registrar um grande evento magmático não relacionado ao LMO 16 ; um desses eventos possíveis é um grande impacto, por exemplo, aquele que formou a Bacia do Polo Sul-Aitken (SPA) 8 .

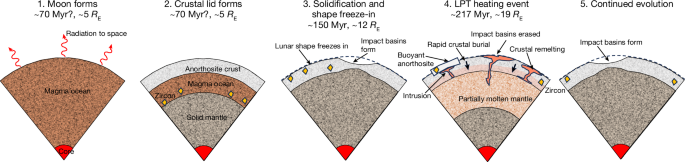
Aqui argumentamos que a idade de aproximadamente 4,35 Ga registra um episódio de aquecimento de maré, e não está diretamente ligada à formação da Lua ou à cristalização do oceano de magma original pós-impacto. O aquecimento de maré foi proposto anteriormente como uma explicação para algumas das características da crosta de comprimento de onda longo da Lua 23 . A Lua aquecida pela maré era um corpo de "tubo de calor" semelhante à lua Io de Júpiter, no qual o calor é advectado pelo derretimento quente que se intromete ou irrompe na superfície, em vez de ser conduzido 24 , 25 . Nesta imagem, o derretimento parcial percola rapidamente através do manto lunar, causando um reequilíbrio isotópico generalizado. A erupção contínua de material impede o desenvolvimento de um verdadeiro oceano de magma 26 e resulta em rápido soterramento e/ou reaquecimento da crosta. Conforme mostrado abaixo, esses processos geralmente devem resultar na redefinição térmica dos sistemas isotópicos frequentemente usados ​​para datar amostras lunares, talvez além daqueles em alguns zircões próximos à superfície. Como tal, um evento de refusão impulsionado pela maré em cerca de 4,35 Ga resolve paradoxos cronológicos lunares existentes e fornece informações sobre como a dissipação da maré na Terra variou ao longo do tempo. A Figura 1 resume nossa linha do tempo prevista de eventos.

Fig. 1: Cronograma hipotético de eventos.
figura 1

O momento da formação da Lua e do congelamento inicial do oceano de magma é incerto. Os zircões se formam durante os estágios finais da cristalização do LMO e são então transportados para cima durante as erupções. A Lua provavelmente se formou por volta de 5  RE ( ref. 53 ) e sua forma congelou por volta de 12  RE (veja o texto ) e não foi modificada pelo evento de aquecimento de maré posterior (o LPT) por volta de 19  RE . No entanto, o intenso vulcanismo e reaquecimento e/ou soterramento associados a este evento redefiniram todos os cronômetros da crosta , exceto os zircões relíquias, e apagaram as bacias de impacto pré-existentes. Aqui, o tempo em milhões de anos (Myr) é contado para a frente a partir da formação do Sistema Solar em 4.568 Myr antes do presente.

Imagem em tamanho real

Refusão durante a transição do plano de Laplace em 4,35 Ga

Três episódios possíveis de aquecimento de maré da Lua podem ser identificados: a ressonância de evecção, em aproximadamente 8 raios da Terra ( R E ) 27 , 28 , 29 ; a transição do plano de Laplace (LPT), em 16–22  R E (ref. 9 ) e as ressonâncias interna e externa 3:2 associadas 30 ; e a transição do estado de Cassini, em 30–34  R E (ref. 31 ). Essas ressonâncias ocorrem, respectivamente: quando o período de precessão da órbita da Lua é igual a um ano; quando os efeitos do Sol e da Terra na precessão orbital da Lua são iguais; e quando os períodos de rotação lunar e precessão da órbita são iguais. Dessas transições, a transição do estado de Cassini ocorre no maior semieixo maior e, portanto, a magnitude do aquecimento de maré é baixa. Os valores típicos são menores que 0,1 W m −2 (ref. 32 ), o que dificilmente desencadeará o derretimento generalizado da Lua. Por razões explicadas abaixo, a passagem da Lua pela ressonância de evecção provavelmente não é o principal impulsionador da refusão, simplesmente porque, para ocorrer em 4,35 Ga, exigiria que a Terra primitiva fosse muito não dissipativa, ainda menos que Júpiter, o que é implausível. Por essas razões, focamos aqui no LPT, que foi originalmente proposto para explicar a alta inclinação da órbita da Lua 9 .

A taxa de aquecimento de maré máxima durante o LPT é estimada em 10 14 –10 15  W (3–30 W m −2 ) por algumas a várias dezenas de milhões de anos 9 , 30 , 33 . A principal razão para a grande liberação de energia é que uma alta excentricidade orbital leva a um forte aquecimento de maré e uma rápida diminuição no semieixo maior lunar. A faixa de fluxo de calor durante o LPT pode ser comparada com a taxa atual de produção de calor de maré em Io de cerca de 2,5 W m −2 (ref. 34 ), indicando que a Lua experimentou fluxos de calor semelhantes a Io ou maiores durante o LPT.

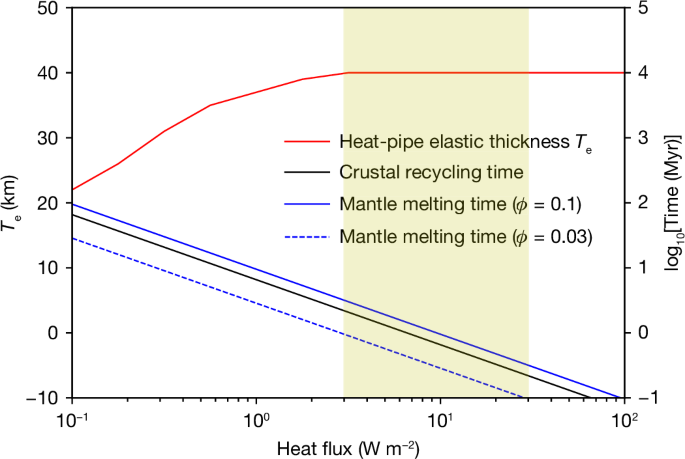
Esses altos fluxos de calor implicam em derretimento prodigioso do manto e vulcanismo. Assumindo que o calor gerado pela maré é removido do manto por meio da convecção do derretimento, podemos calcular quanto tempo leva para todo o manto ser fluxado através da região de derretimento ( Métodos ). A Figura 2 mostra que, para os fluxos de calor estimados do LPT, essa escala de tempo é da ordem de alguns milhões de anos, dependendo da fração de derretimento. Assim, ao longo da duração do evento de aquecimento do LPT 9 , 30 , esperamos que todo o manto seja parcialmente refundido algumas vezes. No entanto, devido à rápida remoção do derretimento, não esperamos que um oceano de magma real se forme 26 .

Fig. 2: Escalas de tempo de reciclagem e fusão e espessura elástica em função do fluxo de calor.
figura 2

A caixa sombreada denota o fluxo de calor de maré inferido durante o LPT 9 . Uma Lua de tubo de calor pode reter uma camada elástica espessa enquanto recicla toda a crosta e derrete novamente todo o manto em um tempo curto em comparação com a duração de alguns a dezenas de milhões de anos de um evento de aquecimento de maré. A espessura da crosta é considerada 40 km e ϕ é a fração média de derretimento do manto. Mais detalhes podem ser encontrados em Métodos .

Dados de origem

Imagem em tamanho real

Reciclagem crustal e redefinição de zircão

O derretimento produzido durante o LPT pode ser principalmente irrompido na superfície ou intrudido dentro da crosta; diferentes regiões da Lua serão dominadas por intrusão ou extrusão dependendo do contraste de densidade local entre o derretimento e a crosta 35 . Blocos crustais anortosíticos preexistentes, sendo de baixa densidade, provavelmente serão dominados pela intrusão.

Para casos de membros finais onde todos os derretimentos são erupcionados para a superfície, o material da crosta é continuamente enterrado e advectado para baixo por lavas em erupção. Um enterramento suficientemente profundo resultará em redefinição térmica e, eventualmente, refusão. A escala de tempo característica para redefinir toda a crosta para é simplesmente para =  h  c / u , onde h c é a espessura da crosta e u é a velocidade de fusão vertical média da área. A Figura 2 plota o tempo de reciclagem da crosta como uma função do fluxo de calor e mostra que para a faixa LPT de 3–30 W m −2 , esse tempo é de cerca de 0,1–1 Myr ( Métodos ). Dada a provável duração do LPT de alguns a dezenas de milhões de anos 9 , 30 , 33 , a reciclagem completa é esperada, de modo que as idades finais da crosta registradas nessas regiões serão simplesmente o momento em que a reciclagem conduzida pelo LPT cessou.

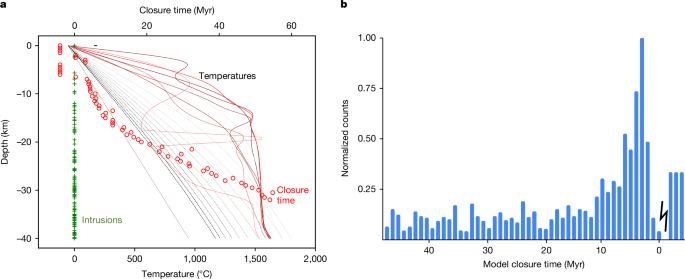
Para áreas que experimentam vulcanismo intrusivo em vez de extrusivo, criamos um modelo simples de evolução térmica condutiva para estudar os efeitos de múltiplas intrusões e rastrear como essas intrusões redefinem as idades registradas por rochas e zircões ( Métodos ). A Figura 3a mostra instantâneos de um modelo de exemplo. A crosta aquece enquanto intrusões (cruzes verdes) são adicionadas ao longo de um período de 3,5 Myr apropriado para o LPT (linhas vermelhas) e, posteriormente, esfria (linhas cinza e preta). Os zircões (círculos vermelhos) registram um tempo de fechamento chumbo-chumbo (Pb-Pb) (relativo ao tempo de início do modelo) dependendo de seu histórico de resfriamento. Alguns zircões próximos à superfície (idades negativas) nunca são redefinidos porque esfriam muito rápido; zircões profundamente assentados esfriam lentamente e, portanto, registram uma ampla gama de tempos de fechamento. No meio, há um acúmulo de idades em torno de 3–5 Myr (perto do tempo em que o aquecimento termina neste modelo específico), porque esta região esfria rapidamente assim que o episódio de aquecimento termina. A Figura 3b plota um histograma de tempos de fechamento Pb–Pb do modelo de zircão usando 30 realizações, semelhante à Fig. 3a . Descobrimos que há um pico na distribuição em 3–5 Myr, e uma pequena fração (cerca de 12%) dos zircões não são redefinidos. Esses resultados do modelo — um pico estreito 8 e alguns zircões antigos 5 , 7 — assemelham-se fortemente às características dos zircões lunares reais.

Fig. 3: Efeito das intrusões nas idades de fechamento Pb-Pb do zircão.
figura 3

O aquecimento de maré e as intrusões começam em 0 Myr e terminam em 3,5 Myr. a , Uma única realização do nosso modelo térmico. As linhas vermelhas sólidas mostram temperaturas em tempos igualmente espaçados de 0 Myr a 3,5 Myr; as linhas tracejadas cinza e preta de 5 Myr a 55 Myr. As cruzes verdes mostram as profundidades de intrusões individuais, onde aqui a altura da escala de intrusão é de 20 km. Os círculos vermelhos denotam o tempo de fechamento Pb–Pb para zircões de raio de 50 μm. Valores negativos indicam zircões que nunca são redefinidos. Aqui, assumimos uma velocidade de advecção de fusão u  = 6 cm ano −1 e a espessura da intrusão é de 2 km ( Métodos ). b , Histograma do tempo de fechamento Pb–Pb de 30 realizações, onde a contagem é normalizada para o maior valor. Tempos de fechamento negativos significam que os zircões nunca foram redefinidos, então a distribuição de idades é arbitrária. Note-se que o pico pronunciado é aproximadamente coincidente com o fim do evento de aquecimento de maré.

Dados de origem

Imagem em tamanho real

Além dos zircões, o aquecimento de maré durante o LPT resolve outros paradoxos na cronologia da Lua. Primeiro, basaltos de mar, FANs e amostras ricas em KREEP plotam ao longo de um único isócrono de 146 Sm– 142 Nd 4 , 36 , que foi interpretado para indicar que essas amostras estavam em equilíbrio isotópico em aproximadamente 4,35 Ga. Essas amostras se originam de várias profundidades dentro da Lua, variando das primeiras dezenas de quilômetros até algumas centenas de 1.000 km (refs. 37 , 38 ). Consequentemente, atingir o equilíbrio isotópico para um volume tão significativo da Lua só é possível por convecção em larga escala de fusão. Isso, combinado com a ocorrência generalizada de idades de aproximadamente 4,35 Ga entre amostras lunares, tem sido até agora atribuído a uma formação tardia da Lua e rápida solidificação do LMO 4 , 16 . No entanto, modelos térmicos sugerem um LMO de vida mais longa, que deveria ter produzido produtos de cristalização com idades distintas 17 . Um evento de aquecimento de maré explica tanto a preponderância de idades lunares de aproximadamente 4,35 Ga 16 quanto o equilíbrio isotópico em grandes porções da Lua 4 , dado que esse evento teve vida curta (algumas dezenas de milhões de anos no máximo 9 , 30 , 33 ) com relação às incertezas das idades lunares.

Em segundo lugar, a suíte Mg lunar parece derivar de reservatórios distintos do LMO, incluindo cumulados máficos dos estágios iniciais da solidificação do LMO, cumulados ricos em plagioclásio semelhantes a FANs e KREEP. Assim, a suíte Mg deve ter se formado por refusão após a cristalização inicial do LMO 37 . As idades de cristalização das rochas da suíte Mg também se agrupam em torno de aproximadamente 4,35 Ga, o que até agora foi explicado pela refusão devido à reviravolta do cumulado imediatamente após a rápida solidificação do LMO 16 . No entanto, a refusão de maré da Lua resultará na intrusão de derretimento em qualquer crosta pré-existente, explicando naturalmente o estreito vínculo temporal entre as rochas da suíte Mg e as FANs formadas anteriormente. Nossos modelos mostram que essas intrusões resultam na redefinição de idades para FANs próximas (Extended Data Fig. 1 ), consistente com as idades indistinguíveis de FANs e rochas da suíte Mg. Além disso, este cenário permite a preservação de idades mais antigas para aquelas FANs que permaneceram mais distantes de qualquer intrusão, embora as evidências atuais para tais rochas sejam fracas 39 .

Embora, em princípio, a Bacia SPA 8 ou a mais antiga e prevista Bacia Procellarum 40 pudessem ter causado o evento de redefinição registrado nas idades lunares de aproximadamente 4,35 Ga, modelos e análises recentes documentados em Métodos não fornecem forte suporte para essas ideias. Em nosso modelo, a Bacia SPA deveria ser mais jovem do que 4,35 Ga, porque, do contrário, teria sido apagada.

Implicações para a evolução inicial da Lua

Uma refusão induzida pela maré da Lua em aproximadamente 4,35 Ga é consistente com várias características proeminentes da Lua, incluindo a sobrevivência da protuberância fóssil da Lua, a ausência de antigas bacias de impacto e as histórias acrecionárias tardias díspares da Terra e da Lua. A Lua parece ter "congelado" sua forma em alguma época anterior, quando estava mais próxima da Terra e tinha características orbitais ou rotacionais diferentes 10 , 41 . Embora os detalhes sejam controversos, o congelamento nesta protuberância fóssil requer o desenvolvimento de uma camada elástica rígida, que não deve ser interrompida por um evento posterior de aquecimento de maré. É importante ressaltar que uma das características de um corpo de tubo de calor extrusivo é que a maior parte da crosta a qualquer momento é fria e rígida 24 , permitindo assim que uma protuberância fóssil persista.

Um estudo anterior 10 descobriu que a protuberância fóssil pode ser explicada se uma camada elástica de 12,8 km de espessura se desenvolveu quando a Lua estava a uma distância de 13  R E , enquanto uma espessura elástica T e de 25 km requer um semieixo maior de 16  R E . Assim, a figura fóssil foi provavelmente estabelecida antes do LPT. Se T e tivesse diminuído abaixo desses valores posteriormente, a protuberância fóssil teria sido reduzida. No entanto, a Fig. 2 mostra que o T e inferido para uma Lua de tubo de calor extrusivo durante o LPT (linha vermelha sólida) pode ser de até 40 km e, portanto, permitir a sobrevivência da protuberância fóssil. As intrusões reduziriam esse valor, mas ainda permitiriam que uma camada fria e rígida persistisse 25 .

Embora a Lua seja canonicamente craterizada, com cerca de 50 bacias de impacto, modelos dinâmicos sugerem que ela deve hospedar mais 12 . Um estudo recente sugeriu que todas as bacias e crateras formadas antes de 4,35–4,41 Ga foram apagadas 13 . Alguns impactos antigos podem não ter sido registrados porque ocorreram enquanto um oceano de magma subterrâneo estava presente 42 . Mas a refusão no manto e o vulcanismo e ressurgimento massivos associados ao evento de aquecimento de maré de aproximadamente 4,35 Ga fornecem uma maneira alternativa de apagar o histórico de bombardeio anterior da Lua e explicar a população observada de bacias e crateras.

Finalmente, um quebra-cabeça sobre a Lua é a concentração muito menor de elementos altamente siderófilos (HSEs) em seu manto em comparação com a Terra 14 . Explicações anteriores para essa característica incluem acreção tardia desproporcional de grandes objetos para a Terra 43 e remoção tardia de HSE do manto lunar durante a cristalização lenta do oceano de magma encerrada pela reviravolta do manto 12 . Nosso modelo de refusão oferece uma alternativa, como segue. Após a cristalização do oceano de magma original, impactos subsequentes terão metal encalhado no manto lunar 44 . Uma refusão posterior do manto terá remobilizado esse metal, que eliminaria os HSEs à medida que descem para o núcleo lunar. Se o manto lunar perdeu todos os HSEs acumulados antes de 4,35 Ga, as concentrações de HSE lunares do modelo fornecidas por impactos subsequentes correspondem às medidas, assumindo 30% de retenção de material de impacto na Lua 45 . É impressionante que esse argumento, baseado apenas em simulações dinâmicas, produza um tempo de início para retenção de HSE de aproximadamente 4,35 Ga (refs. 12 , 13 , 45 ), consistente com nossa hipótese de refusão.

Implicações para a idade da Lua

A interpretação das idades lunares de aproximadamente 4,35 Ga como resultado do aquecimento de maré em vez da cristalização LMO original implica que a Lua se formou antes. Como o LPT ocorre em um semieixo maior específico (16–22  R E ) 9 , ao vinculá-lo a um evento de refusão em 4,35 Ga podemos fazer inferências sobre a evolução orbital inicial da Lua. O principal impulsionador da migração lunar é a dissipação de maré na Terra, parametrizada pelo fator de dissipação Q E . A migração inicial foi rápida e provavelmente em uma escala de tempo comparável àquela em que a Terra estava evoluindo durante sua recuperação do impacto de formação da Lua. Consequentemente, prever Q E a partir dos primeiros princípios é desafiador e depende de fatores pouco conhecidos, como a escala de tempo para a cristalização do oceano de magma da Terra e a espessura e duração de qualquer atmosfera inicial 46 , 47 .

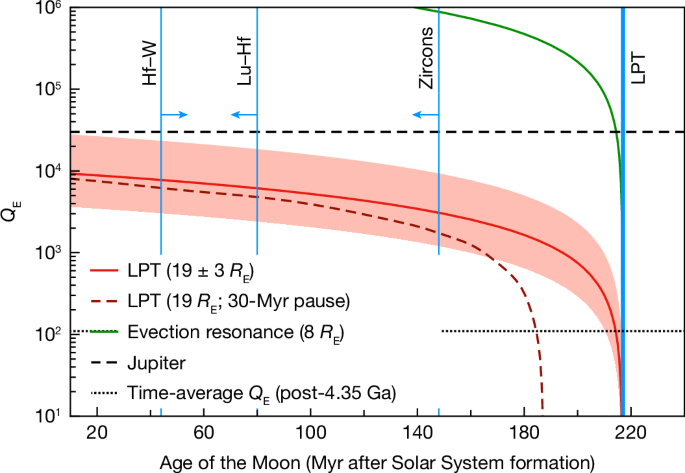
No entanto, podemos deduzir um Q E médio aplicável a este período de evolução lunar ( Métodos ). A linha vermelha na Fig. 4 mostra o trade-off entre o momento em que a Lua se formou e o Q E médio necessário para que ela atingisse 19  R E em 4,35 Ga. A incerteza na distância LPT (±3  R E ) é indicada pelo sombreamento vermelho. Um tempo de formação inicial permite uma Terra menos dissipativa ( Q E mais alto ). A Lua pode ter parado no LPT por algumas dezenas de milhões de anos 9 , 30 , 34 , mas a Fig. 4 mostra que isso tem muito pouco efeito no Q E, exceto se a Lua se formou tarde (o que é descartado pelas idades do zircão; veja abaixo). Os valores de Q E derivados são geralmente muito mais altos (menos dissipativos) do que a Terra sólida atual, para a qual Q E  ≈ 300 (ref. 48 ). No entanto, eles são menores que o Q de Júpiter, que foi medido em aproximadamente 3 × 10 4 usando astrometria 49 . Não se esperaria que um corpo sólido de silicato, mesmo que totalmente fundido, fosse menos dissipativo que um gigante gasoso como Júpiter 50 , e então o Q de Júpiter pode ser tomado como limite superior estrito para Q E .

Fig. 4: Restrições na dissipação da Terra primitiva.
figura 4

Fator de dissipação Q E mostrado como uma função do tempo de formação da Lua para a Terra atingir 19 ± 3  R E em 4,35 Ga (linha vermelha). A linha vermelha tracejada inclui uma pausa no LPT de 30 Myr (veja o texto). As linhas pretas horizontais indicam duas restrições em Q E : o valor médio após 4,35 Ga (veja o texto); e o valor medido de Q para Júpiter 49 , que consideramos um limite superior para a Terra. As linhas azuis verticais denotam o tempo do LPT, idades Pb–Pb de zircões individuais raros 5 , 7 , uma idade modelo Lu–Hf para a formação de KREEP derivada de zircões lunares 6 , e a idade modelo Hf–W para a formação do núcleo na Terra, que fornece o tempo mais antigo possível de formação da Lua 52 .

Dados de origem

Imagem em tamanho real

A Figura 4 mostra que o intervalo de tempo entre a formação da Lua e o início do LPT é incerto; pode ser de até cerca de 200 Myr ou tão curto quanto cerca de 10 Myr. O último intervalo é consistente com modelos de evolução orbital de longo prazo 51 , onde a Lua atinge 20  R E cerca de 10 Myr após a formação. No entanto, também são mostradas na Fig. 4 as idades dos zircões lunares mais antigos, bem como a idade do modelo Lu-Hf da formação de KREEP, conforme determinado em zircões lunares. Como esses zircões se formaram após diferenciação substancial da Lua 6 , a Lua deve ter se formado antes que esses zircões se cristalizassem em aproximadamente 4,43 Ga, ou seja, pelo menos aproximadamente 80 Myr antes do LPT. Por outro lado, um limite inferior para o tempo de formação da Lua é fornecido pelo modelo Hf–W de dois estágios de formação do núcleo na Terra de 4,533 Ga, que fornece o tempo mais antigo em que a formação do núcleo pode ter cessado 52 . Como se acredita que o último evento de formação do núcleo na Terra tenha sido desencadeado pelo impacto de formação da Lua, essa idade do modelo também fornece o tempo mais antigo em que a Lua pode ter se formado, que é cerca de 180 Myr antes do LPT.

Embora o conhecimento pobre de QE limite nossa capacidade de datar precisamente a formação da Lua usando o tempo do LPT, nosso modelo sugere fortemente que a Lua se formou muito antes de 4,35 Ga, provavelmente na faixa de 4,43–4,53 Ga. Modelos dinâmicos mostram que a formação de planetas terrestres é suficientemente estocástica para permitir um evento de formação da Lua tão tarde quanto cerca de 200 Myr, mesmo começando de uma distribuição concentrada de material em torno de 1 UA (ref. 11 ) . No entanto, uma fase tão prolongada de formação de planetas terrestres normalmente leva a sistemas que são dinamicamente superexcitados, e a quantidade de material acumulado pela Terra após a formação da Lua é muito pequena para explicar as abundâncias de HSEs no manto da Terra 11 , 18. A formação da Lua em aproximadamente 4,5 Ga resolveria esses problemas, mas neste caso a Lua teria acumulado muito mais bacias de impacto e mais material acumulado tardiamente do que o observado 12 , 13 . Assim, nossa proposta de uma formação lunar inicial seguida por uma fusão tardia, impulsionada pelas marés, parece uma maneira provável de reconciliar essas observações aparentemente contraditórias.

Métodos

Lua de tubo de calor

A equação de convecção-difusão em uma geometria cartesiana bidimensional sem aquecimento interno é escrita 24

∂𝑇∂𝑡=𝜅∂2𝑇∂𝑧2−𝑢∂𝑇∂𝑧

onde T é a temperatura, κ é a difusividade térmica, u é a velocidade descendente da crosta devido ao enterramento e z é positivo para baixo. Em estado estacionário, a solução é

𝑇=𝑇s+(𝑇b−𝑇s)(e𝑢𝜅ℎ𝑐−1)(e𝑢𝜅𝑧−1)
(1)

onde T s é a temperatura da superfície e T b é a temperatura na base da crosta (espessura h c ). Note-se que esta expressão se reduz à equação de condução padrão no limite em que u é pequeno. O fluxo de calor condutivo na base da crosta é F  = ( T b  −  T s ) u / κ , que pode ser reescrito como ρC p u ( T b  −  T s ), o fluxo de calor advectivo (os dois devem se equilibrar em estado estacionário). Aqui ρ é a densidade e C p é a capacidade de calor específica, modificada para incluir um efeito de calor latente (isto é, aumentamos a capacidade de calor específica usual com um termo L /( T b  −  T s ) onde L é o calor latente).

A isoterma que define a base da camada elástica no material do manto oceânico na Terra está em cerca de 720 K (ref. 54 ). Usamos essa isoterma e a equação ( 1 ) para determinar a espessura elástica como uma função do fluxo de calor. Para um fluxo de calor especificado F , também podemos resolver para u e, assim, derivar o tempo de reviravolta t c / u . Assim, se F  = 10 W m −2 , obtemos u  = 0,06 m yr −1 e um tempo de reviravolta da crosta de 0,67 Myr.

A escala de tempo de fusão do manto pode ser derivada da seguinte forma. A taxa de fluxo de material na superfície é 4π u , e se a fração de fusão for ϕ então a taxa na qual o material do manto é fluxado através da zona de fusão é 4π u / ϕ , onde R M é o raio lunar (1.740 km). O volume total do manto é aproximadamente o de toda a Lua, 4/3π . Assim, a escala de tempo para fluir todo o manto através da zona de fusão é R M ϕ /3 u . Se ϕ  = 0,1 e u  = 0,1 m ano −1 , então a escala de tempo é 0,58 Myr, comparável à escala de tempo de reviravolta da crosta.𝑅𝑀2{R}_{M}^{2} {R}_{M}^{3}𝑅𝑀2𝑅𝑀3

Os parâmetros adotados são os seguintes: ρ  = 2.600 kg m −3 , k  = 2 W m −1  K −1 (ref. 17 ), L  = 450 kJ kg −1 , C p  = 1.200 J kg −1  K −1 , T s  = 220 K e T b  = 1.500 K. Em nossos modelos de base, tomamos h c  = 40 km (ref. 55 ). Foi sugerido anteriormente que a Lua primitiva era um corpo de tubo de calor 56 , mas não no contexto de um evento de aquecimento de maré.

Reinicialização intrusiva

Resolvemos uma equação de condução de calor de diferença finita unidimensional estática simples na qual as intrusões são adicionadas em intervalos. Para levar em conta a natureza aleatória do comportamento intrusivo, atribuímos uma distribuição de probabilidade para a altura acima da base da crosta z ′ na qual a intrusão ocorre, onde a probabilidade é proporcional a exp(− z ′/ δ ), com δ uma altura de escala especificada pelo usuário. Um valor baixo de δ significa que as intrusões estão concentradas em direção à base da crosta. Para simplificar, assumimos uma única espessura de intrusão característica Δ d (um múltiplo inteiro do espaçamento da grade Δ z ) e um intervalo de tempo característico entre as intrusões Δ t . Uma vez que Δ d é especificado, Δ t é então determinado pelo requisito de que Δ d /Δ t  =  u , onde u é calculado conforme descrito acima.

Em intervalos Δ t , nós intrudimos uma intrusão de espessura Δ d em um ponto de grade escolhido aleatoriamente na crosta. O material intrudido recebe uma temperatura inicial de T m e a temperatura da superfície T s é mantida constante. O fluxo de calor basal F b também é mantido constante em um valor apropriado para a Lua antes do evento de aquecimento; a suposição é que o calor de maré produzido no manto está sendo transportado por advecção (ascensão do derretimento) em vez de condução. À medida que as intrusões prosseguem, a temperatura basal aumentará. O aquecimento de maré começa no tempo zero do modelo, termina após 3,5 Myr e então continuamos o modelo até 55 Myr. O passo de tempo de diferença finita é definido como 0,3Δ z 2 / κ para satisfazer o critério de Courant, com Δ z  = 0,5 km. Os parâmetros térmicos são os mesmos do modelo de tubo de calor (acima); outros valores de parâmetros nominais são: T m  = 1.550 °C, F b  = 50 mW m −2 e Δ d  = 2 km.

Usamos o mesmo modelo para investigar até que ponto o aquecimento pelas intrusões resulta na redefinição das idades de zircão Pb–Pb. Aqui, implementamos um modelo simples para difusão para rastrear o tempo em que a perda difusiva efetivamente cessa; esse tempo dará a idade registrada.

Para um zircão com difusividade constante D , o tempo τ que leva para a perda difusiva penetrar uma distância p no cristal é dado por p  = (π 2 Dτ ) 1/2 , onde π 2 é um fator apropriado para nosso cristal (assumidamente esférico) 57 . Na realidade, D é dependente da temperatura. Portanto, diferenciamos a relação constante- D para obter

Δ𝑝≈𝜋2(𝐷𝑡)1/2Δ𝑡

Aqui Δ p é a mudança na distância de penetração ao longo de um intervalo de tempo Δ t . Enquanto D estiver mudando lentamente, podemos usar esta expressão para determinar como p ( t ) aumenta com o tempo. Uma vez que p ( t ) é igual à metade do raio do cristal, 7/8 do volume do cristal terá sofrido perda de Pb, a redefinição é assumida como tendo ocorrido e no próximo passo de tempo reiniciamos o cálculo definindo p  = 0 e t  = Δ t (para evitar uma singularidade na origem). Desta forma, podemos rastrear quando a perda de Pb efetivamente cessa. Assumimos que a difusividade é dada por D 0 exp(− Q / RT ), onde para Pb D 0  = 0,11 m 2  s −1 e Q  = 550 kJ mol −1 (ref. 58 ) e R é a constante dos gases. A aplicação desta abordagem com uma taxa de resfriamento de 10 °C Myr −1 produz temperaturas de fechamento de 968 °C e 877 °C com raios de zircão de 100 μm e 10 μm, respectivamente. Esses valores se comparam favoravelmente aos valores de cerca de 990 °C e 895 °C mostrados na Fig. 13 da ref. 58. Em nosso modelo nominal, assumimos um raio de zircão de 50 μm.

Para uma dada profundidade dentro da Lua, sabemos como a temperatura está evoluindo com o tempo e, portanto, podemos calcular D ( t ) e o tempo em que a última redefinição ocorre para quaisquer zircões presentes naquela profundidade. Essa abordagem é a base das idades do zircões mostradas na Fig. 3 , onde uma distribuição inicial uniforme de zircões com profundidade é assumida. Os resultados mudam minimamente (<1%) se dobrarmos ou reduzirmos pela metade o raio do zircões. Se as intrusões forem mais concentradas em direção à base da crosta, a fração de zircões que não passam por redefinição aumenta, como esperado (Dados Estendidos Fig. 2 ). A mesma análise para Hf (que difunde mais lentamente) mostra que cerca de 30% dos zircões não são redefinidos para nossos parâmetros nominais do modelo. Eventos de aquecimento de duração mais longa resultam em mais redefinições de rochas (Dados Estendidos Fig. 3 ).

Evolução orbital lunar

A dissipação na Terra impulsiona a evolução para fora da Lua, enquanto a dissipação na Lua circulariza a órbita da Lua e também pode impulsionar a evolução orbital para dentro 59 . Abaixo, assumimos que a dissipação na Terra domina. A evolução do semieixo maior da Lua a é então dada por 60 :

d𝑎d𝑡=3𝑘2E𝑄E𝑚𝑀(𝑅E𝑎)5𝑛𝑎
(2)

Aqui k 2E e Q E são o número de Love de maré e o fator de dissipação da Terra, m e M são a massa da Lua e da Terra, respectivamente, R E é o raio da Terra e n é o movimento médio da órbita lunar. Tomamos M  = 6 × 10 24  kg, m  = 7,4 × 10 22  kg, R E  = 6.400 km e k 2E  = 0,97. O último valor é o apropriado para uma Terra sem resistência (por exemplo, derretida), em vez de tomar o valor atual de 0,299, que é devido à rigidez do manto atual 59 . Uma limitação de todos os modelos existentes do LPT 9 , 30 , 34 é que eles assumem valores constantes de Q e k 2 ; antecipamos que a incorporação de feedbacks térmico-orbitais encurtará o período de aquecimento de maré.

O papel dos impactos antigos

Consideramos se é possível que um grande impacto que formou a Bacia SPA ou a Bacia Procellarum 40 , mais antiga e prevista , tenha causado o evento de redefinição registrado nas eras lunares de aproximadamente 4,35 Ga. Em relação à Bacia SPA, há três possibilidades. A primeira é que o ejetado do próprio impacto SPA poluiu a região Apollo, mas os modelos mostram que isso não ocorre 61 . Segundo, o material da camada derretida SPA pode ter sido redistribuído por impactos subsequentes 8 , mas descobrimos que a fração desse material nos locais Apollo era de apenas cerca de 2% (veja abaixo). Terceiro, a Bacia SPA pode ter desencadeado a convecção do manto e o derretimento 62 , mas um problema potencial com esse modelo é que o vulcanismo que ele produz é de longa duração e não geraria obviamente o pico de idades que um curto período de aquecimento de maré gera, e que é observado entre as eras lunares. Esse modelo também implica derretimento focado em um hemisfério, enquanto o nosso argumenta a favor do derretimento global. De notar que o meteorito lunar Kalahari 009 mostra uma idade Pb–Pb de 4,369 ± 0,007 Ga e, com base em fundamentos químicos, acredita-se que derive do lado distante lunar, consistente com nosso modelo de um evento de refusão global em torno de 4,35 Ga (ref. 63 ). Como esse evento provavelmente terá apagado quaisquer bacias pré-existentes, prevemos que a Bacia SPA em si seja mais jovem do que 4,35 Ga.

Finalmente, modelos do impacto que formou a suposta Bacia Procellarum 45 mostram que o derretimento do impacto resultante é localizado e não seria suficiente para causar o tipo de mistura e redefinição global que as amostras lunares parecem exigir. Assim, os modelos atuais não suportam a ideia de impactos serem responsáveis ​​pelo evento de redefinição.

Redistribuição de material da Bacia do SPA

Os locais da Apollo terão recebido material originário da camada de fusão do SPA e redistribuído por impactos subsequentes 8 . Eles também terão recebido material ejetado de outras regiões da Lua. Desejamos comparar as massas relativas dessas duas contribuições. O fator-chave é que a fração de ejeção viajando com uma velocidade particular diminui à medida que essa velocidade aumenta 64 ; assim, impactos mais distantes fornecem uma fração menor de material ejetado em comparação com impactos mais próximos.

Usando o modelo simples de Maxwell 65 , 66 , podemos mostrar que o volume de material V s ejetado a uma velocidade radial que excede um valor especificado u s proporcional ao volume total de material V ejetado é dado por

𝑉s𝑉≈(𝑔𝑅t4𝑍(𝑍−2)𝑢s2)3/2𝑍
(3)

onde g é a gravidade da superfície, R t é o diâmetro da cratera transiente e Z é uma constante. Uma cratera transiente maior produz uma fração maior de material de alta velocidade, mas a sensibilidade é fraca 64 . A velocidade radial mínima u s necessária para uma partícula percorrer uma distância s é dada por ( gs /2) 1/2 .

Precisamos deduzir o raio da cratera transitória R t do raio da cratera observada R f . Para fazer isso, usamos a escala usada na ref. 67 onde

𝑅t=(𝑅c𝜉𝑅f)1/(1+𝜉)
(4)

Aqui R c é o raio de transição da cratera simples-complexa (9 km para a Lua) e ξ é uma constante.

Usamos um catálogo de todas as crateras de impacto que excedem 1–2 km de diâmetro na Lua 68 , um total de 1.296.795 excluindo a própria Bacia SPA. Para calcular o volume de material ejetado de uma região específica por impactos subsequentes, usamos o seguinte algoritmo para cada cratera de impacto. (1) Determine se o centro da cratera de impacto cai dentro da região especificada (por exemplo, a camada de fusão SPA). (2) Se cair, determine a distância do grande círculo s do centro da cratera de impacto até o local alvo. (3) Calcule a velocidade horizontal mínima u s necessária para atingir essa distância. (4) Calcule o raio transitório da cratera R t associado ao raio final medido da cratera R f usando a equação ( 4 ). (5) Use u s , R t e a equação ( 3 ) para calcular o volume de material ejetado a uma velocidade superior a u s em comparação com o volume total de material ejetado.

Este algoritmo pode ser repetido para cada cratera observada para determinar a massa total ejetada da região especificada capaz de atingir o local alvo. Realizamos este algoritmo duas vezes, uma para crateras dentro da camada de fusão SPA e uma para crateras em outros lugares. A razão das duas respostas fornece uma medida de qual fração de todo o material acumulado no local alvo é derivado da camada de fusão SPA. Para nossos valores de parâmetros nominais, encontramos um valor de 1,7%.

Seguimos a ref. 66 e tomamos Z  = 2,71. A equação ( 3 ) então produz um expoente de 0,55, ligeiramente menor do que o intervalo de 0,6–0,85 defendido pela ref. 64. Um valor mais alto produz um valor mais baixo de Z e resulta em uma contribuição menor da bacia SPA. Por exemplo, se tomarmos Z  = 2,2, então a fração de volume é reduzida para 1,4% em comparação com 1,7% para o modelo nominal. Usamos ξ  = 0,22 para reproduzir a relação entre o diâmetro transitório e final da cratera derivado pela ref. 69. Usar um valor menor de ξ  = 0,13 causa uma ligeira redução na fração de volume derivada da Bacia SPA (1,3% em comparação com 1,7%). Tomamos g  = 1,6 m s −2 e usamos a localização (0°, 0°) como uma média apropriada das localizações do sítio Apollo. Variações na longitude ou latitude em ±10° alteram a resposta da fração de volume em menos de 0,1%.