Como Eratóstenes descobriu o formato da Terra há mais de 2 mil anos

Eratóstenes nasceu em Cirene, Grécia, e morreu em Alexandria, Egito, no terceiro século AEC. 

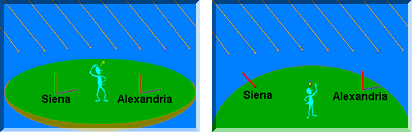
Ele era bibliotecário-chefe da famosa Biblioteca de Alexandria, e foi lá que ele encontrou, num velho papiro, indicações de que ao meio-dia de cada 21 de junho na cidade de Assuã (ou Syene, no grego antigo) 800 km ao sul de Alexandria, uma vareta fincada verticalmente no solo não produzia sombra.

Cultura inútil, diriam alguns. Não para um homem observador como Eratóstenes. Ele percebeu que o fenômeno não ocorria no mesmo dia e horário em Alexandria, e pensou:

Se o mundo é plano como uma mesa, então as sombras das varetas têm de ser iguais. E se isto não acontece é porque a Terra deve ser curva! Mais do que isso.

Quanto mais curva fosse a superfície da Terra, maior seria a diferença no comprimento das sombras. O Sol deveria estar tão longe que seus raios de luz chegam à Terra paralelos.

Varetas fincadas verticalmente no chão em lugares diferentes lançariam sombras de comprimentos distintos.

Eratóstenes decidiu fazer um experimento. Ele mediu o comprimento da sombra em Alexandria ao meio-dia de 21 de junho, quando a vareta em Assuã, ao Sul do Egito, não produzia sombra.

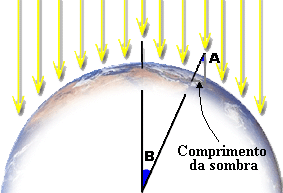
Assim, ele obteve o ângulo A, conforme a figura abaixo.

Eratóstenes mediu A=7° (aproximadamente). Se as varetas estão na vertical, dá para imaginar que se fossem longas o bastante iriam se encontrar no centro da Terra. Preste atenção na figura acima.

O ângulo B terá o mesmo valor de A, pois o desenho do experimento de Eratóstenes se reduz a uma geometria muito simples: se duas retas paralelas interceptam uma reta transversal, então os ângulos correspondentes são iguais.

As retas paralelas são os raios de luz do Sol e a reta transversal é a que passa pelo centro da Terra e pela vareta em Alexandria.

O ângulo B (também igual a 7°), é a uma fração conhecida da circunferência da Terra e corresponde à distância entre Assuã e Alexandria!

Eratóstenes sabia que essa distância valia cerca de 800 km e então pensou: 7° são aproximadamente 1/50 de uma circunferência (360°).

E isso corresponde a cerca de 800 km. Oitocentos quilômetros vezes cinquenta são quarenta mil quilômetros, de modo que deve ser este o valor da circunferência da Terra.

O mundo não é chato

VALOR ENCONTRADO ATUALMENTE: cerca de 40.072 km ao longo da linha do equador. Um erro muito pequeno para uma medida tão simples, e feita há tanto tempo!

Com a circunferência, podemos calcular o diâmetro e o raio ou ainda o volume e a área da superfície, através de fórmulas simples.

Repare que o conhecimento utilizado por Eratóstenes (retas paralelas cortadas por uma transversal) é formalmente adquirido hoje nas aulas de geometria do Ensino Fundamental.

Fica a sugestão para a realização dessa experiência fantástica entre escolas de lugares distantes. Com as facilidades de comunicação de hoje é ainda mais fácil sentir o prazer de usar um raciocínio tão simples e elegante para obter uma medida tão preciosa.

Fonte:

Costa, J. R. V. Eratóstenes e a circunferência da Terra. Astronomia no Zênite, jul 2000.